Visualizing horospheres on hyperbolic groups
This semester I was able to participate in our undergradute research lab, and, relevant to my past work, our project was in the field of geometric group theory. I plan on introducing our project and go over some topics in geometric group theory I haven’t covered before. This project was joint work with Noah Jillson and Katerina Stuopis with our advisors Daniel Levitin and Tullia Dymarz.
If you want to skip the mathematical jargon and see the results, skip to the end.
Hyperbolic geometry
Hyperbolic geometry is an important part of non-Euclidean geometry, where we study spaces that do not satisfy the postulates of Euclidean geometry. In particular, hyperbolic spaces replace Euclid’s fifth postulate with “given a line $L$, and a point $P$ not on $L$, there are multiple lines that are parallel to $L$ and pass through $P$.”
A consequence of this is that hyperbolic space has negative curvature. Intuitively, this means that as go off from a point in two directions, you will end up very far apart. All points in hyperbolic space “look like” a saddle point. There are many ways to represent the hyperbolic plane $\mathbb{H}^2$, one of which is shown in the following figure. However, we are forced to embed them into $\mathbb{R}^2$, so properties like distance and size are not as they appear.
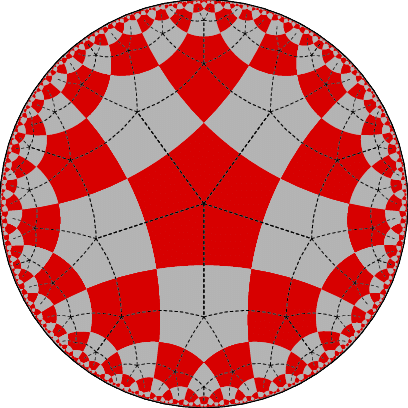
Figure. Tiling the hyperbolic plane with pentagons in the Poincaré disk model. Looking at the dashed lines, we can see that there are $5$ squares at each corner, or $90^\circ\cdot5 = 450^\circ$. This is only possible in hyperbolic space.
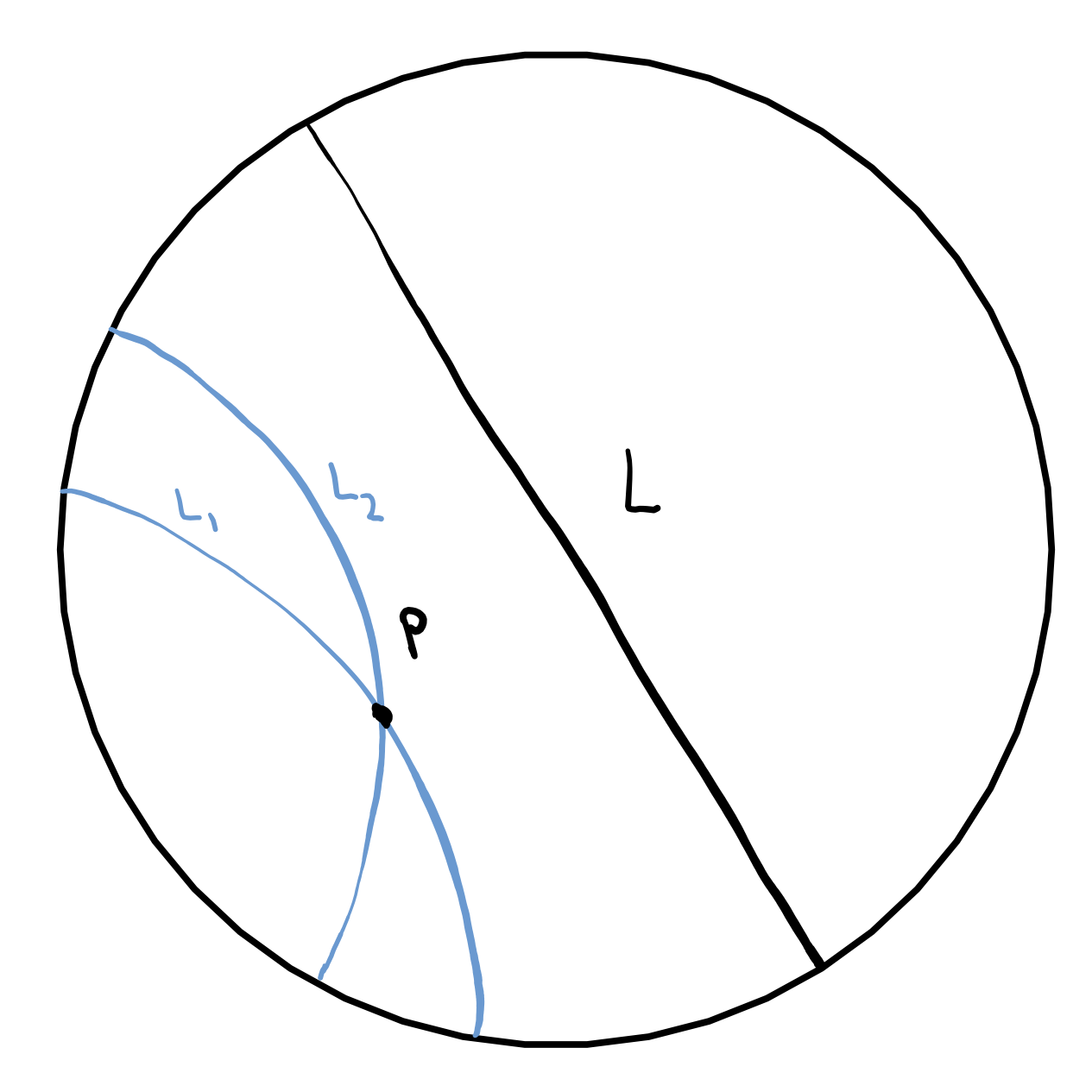
Figure. In the Poincaré disk model, both $L_1$ and $L_2$ are parallel to $L$ and pass through $P$.
Horospheres
Horospheres are a geometric object that are defined on hyperbolic spaces. They formalize the idea of taking a sphere “to infinity.” Formally, we take a geodesic ray $\gamma\colon[0,\infty)\to H$, where $H$ is a hyperbolic space. A geodesic is a path from one point to another where the path is as small as possible. The ray just has the property that any subset of $\gamma$ is a geodesic as well.
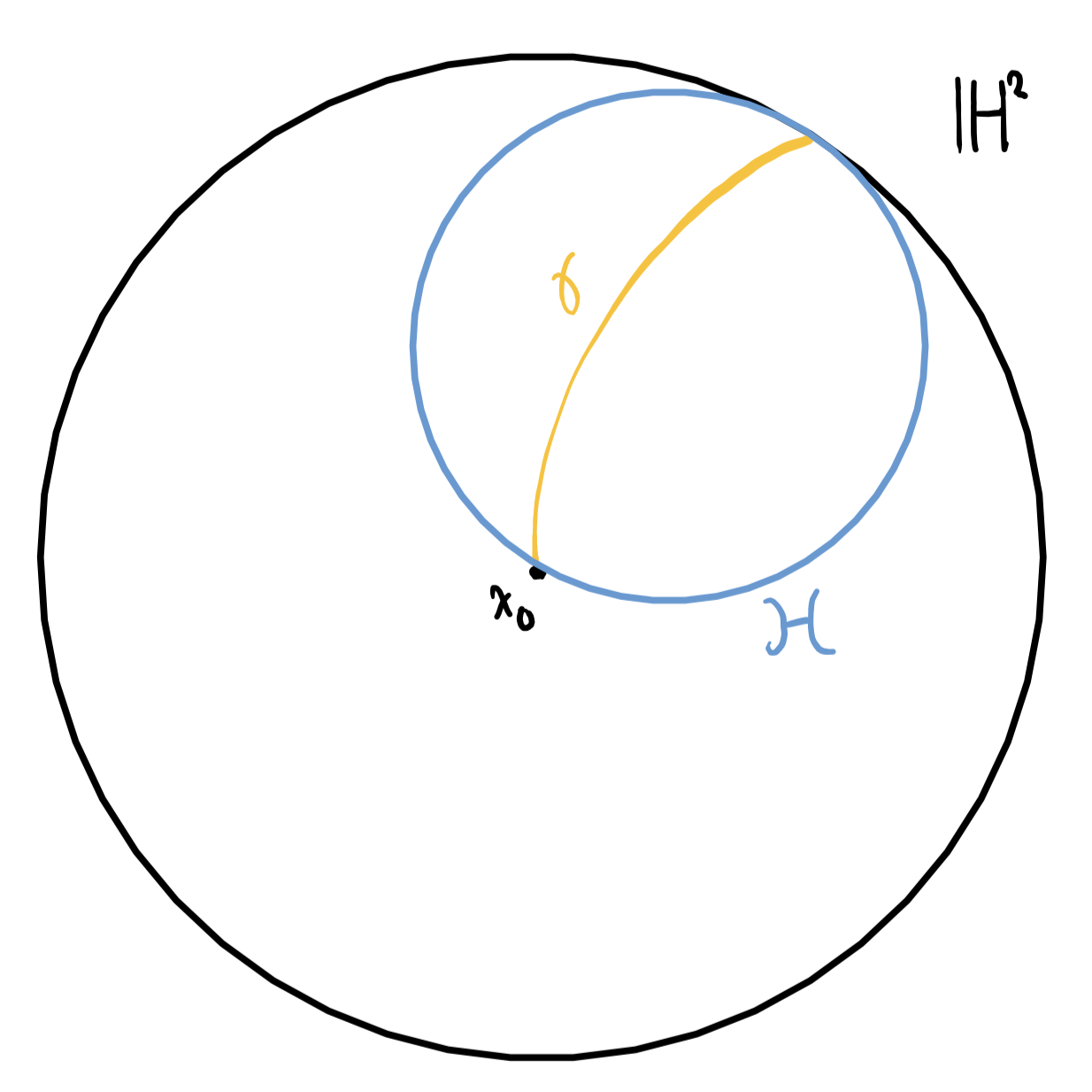
Figure. The (zero-)horosphere along the ray $\color{Goldenrod}\gamma$ is $\color{RoyalBlue}\mathcal{H}$
To formally find all points at this horosphere, we need to use a Busemann function of $\gamma$ relative to $x_0$, which is defined as $$ b_{\gamma,x_0}(x) \coloneqq \lim_{t\to \infty}d(x,\gamma(t))-d(x_0,\gamma(t)). $$ The zero set (the set of all $x$ so that the function evalautes to $0$) is called the $0$-horosphere. It will be assumed that all horospheres mentioned are $0$-horospheres.
Our groups of study: Right-Angled Coxeter Groups
Recall that we can turn groups into labeled, directed graphs through their Cayley graph. By observing the geometric properties of the Cayley graph, we can get algebraic ideas about the group itself (see ends). A hyperbolic group has a hyperbolic Cayley graph. Thus, we can find horospheres on these Cayley graphs.
Definition (Right-Angled Coxeter Groups). Given a defining graph $\Gamma$, which consists of vertices $V$ and edges $E$, we define its associated Right-Angled Coxeter Group (RACG) as the presentation $$ W_{\Gamma} \coloneqq \langle V \mid {\color{LimeGreen}v^2}, {\color{violet}[v_1,v_2]} : v\in V, (v_1,v_2) \in E \rangle. $$
We will refer to $V$ as the letters of $W_{\Gamma}$, and any combination of letters as a word (which is also a group element!). The most important parts of this definition is that $\color{LimeGreen}\text{letters cancel if written twice}$, and $\color{violet}\text{letters commute if they are an edge in the defining graph}$.
Example (Pentagon graph). RACGs tend to represent reflections. In fact, we can relate our group to reflections along the hyperbolic plane. For example, for the tiling shown in the first figure, there is a RACG that represents the reflections along the lines between pentagons. Its defining graph is shown below.
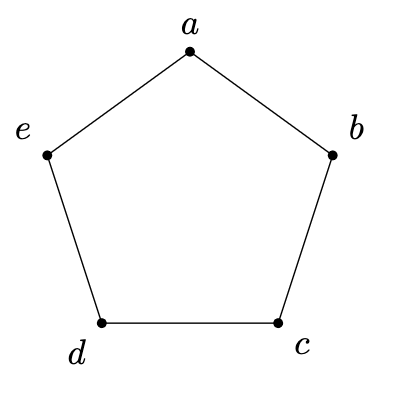
Figure. Defining graph for symmetries of a $5$-square tiling of $\mathbb{H}^2$.
In order to make sure our groups are hyperbolic, we need the following theorem.
Theorem (Moussong). A RACG is hyperbolic if and only if its defining graph does not have a square.
We can prove this in one direction easily. If we assume that the RACG has a square, then we can find a subgroup that is isomorphic to $\mathbb{Z}\oplus\mathbb{Z}$. This is non-hyperbolic, and will therefore violate our requirements for hyperbolicity.
Because of this, we have to make sure that our defining graphs do not have any squares.
Methods: discretizing horospheres
To create our horosphere on RACGs, we first wanted to find a point on the horosphere, and try to expand outwards. We could ran a program to find other words also on the horosphere. To make sure that we didn’t repeat words (like $ab$ and $ba$), we set an order $<$ on equivalent words called ShortLex, which essentially found the shortest, then lexicographically first way to write a word. We would let the program run out to some length and then have it return a list of the words it found.
However, we ended up just having a list of words, but with no clear relation. Our next task was to combine them into a discrete graph. Since words of the horosphere were even distance apart (with respect to the word metric), we connected words that were exactly $2$ apart. In many cases, this connected our graph, and gave some idea of the structure of the horosphere.
Our main work this semester was to extend our program to work with much more complex defining graphs. One defining graph we chose was a triangulation of a torus, which had $21$ nodes.
Results
We were able to put the horosphere data in Mathematica to get pictures of the horospheres.

Figure. Length $4$ horosphere of the pentagon defining graph.

Figure. Length $3$ horosphere of the torus triangulation defining graph.
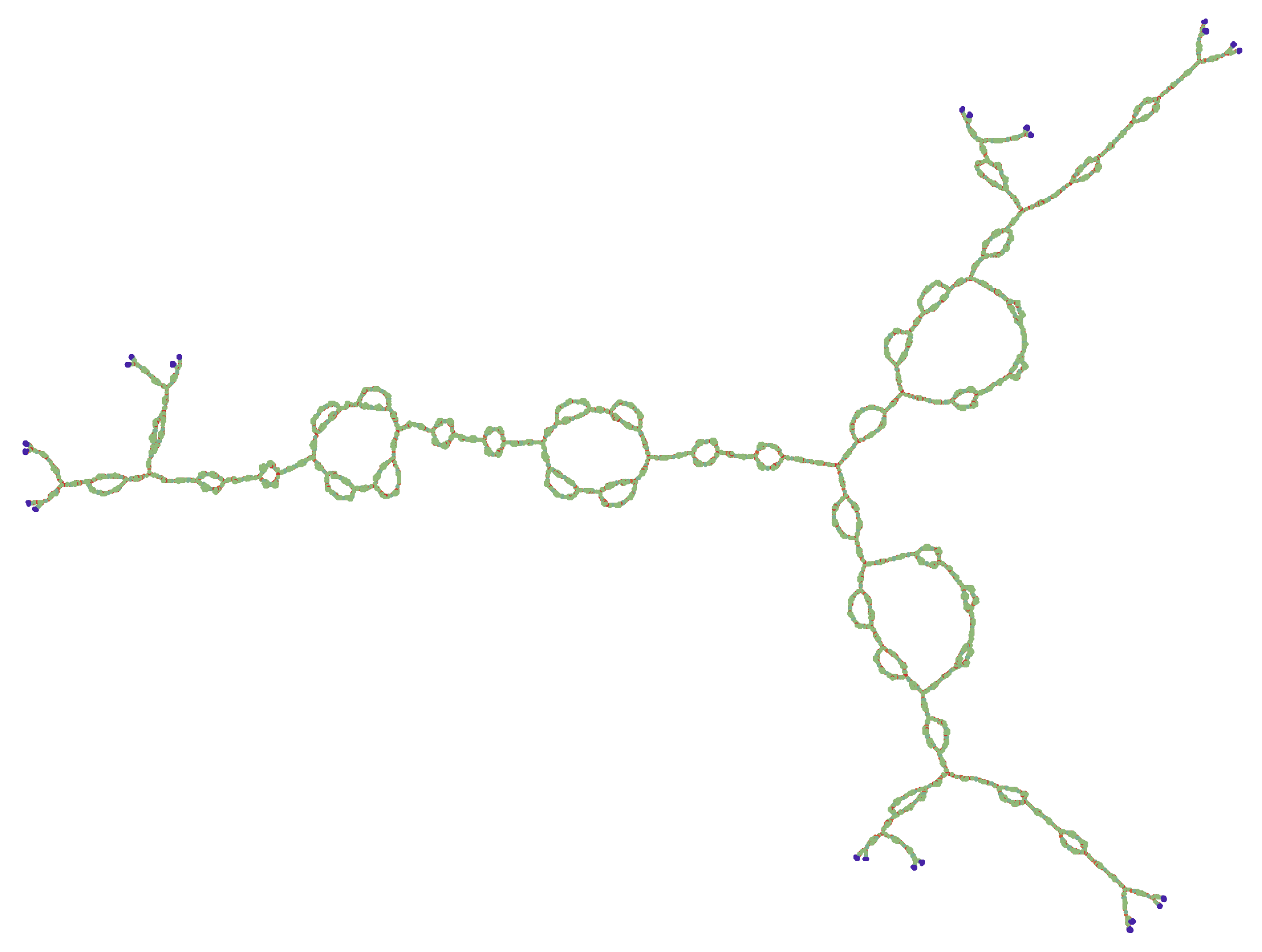
Figure. Length $5$ horosphere of another defining graph (we call it the theta graph because it looks like the letter $\Theta$).
Discussion
We know that finitely generated groups can have either $0$, $1$, $2$, or $\infty$ ends on their Cayley graphs. The horosphere however, is not the entire Cayley graph. We found it can have more interesting numbers of ends (such as $3$ in the $\Theta$ graph). We can prove the number of ends a horosphere is based on our defining graph and which ray we choose, and we now visualize this.
Generating a finite part of the horosphere on a group gives us a discrete visualization of the boundary of that group. The boundary is the set of geodesic rays with the equivalence relation $\sim$ between rays if they are “going the same direction.” The boundary of a hyperbolic space minus a point looks similar to these finite horospheres. In fact, the boundaries of some of our RACGs can be understood as homeomorphic to one of three objects: a $2$-sphere, and two fractal-like surfaces.
The horosphere of the pentagon defining graph looks like a line because the boundary of the group is a circle, and a circle minus a point can be stretched to look like (is homeomorphic to) a line.