A presheaf which is not a sheaf
I’ve been reading Ravi Vakil’s Rising Sea: Foundations of Algebraic Geometry this semester, specifically the second chapter which gives an introduction to sheaf theory. While the first half of the chapter serves to introduce the idea of a sheaf and to convince you that it makes sense geometrically to define it, I would say the meat of the chapter is defining the sheafification of a presheaf and explain how it helps us do homology on sheaves.
Presheaves and sheaves
This year, my courses have been filled with categorical language, so this post will be more abstract than usual.
Definition (Presheaf).
Let $X$ be a topological space. Let $\mathsf{OpenSet}(X)$ be the category of open sets of $X$, ordered by inclusion: objects are open sets $U \subseteq X$, and arrows are inclusion maps $U \xhookrightarrow{} V$. A presheaf of sets (or abelian groups, rings, etc.) is a functor
$$ \mathscr{F}\colon \mathsf{OpenSet}(X)^{\mathrm{op}} \to \mathsf{Set}, $$
where we send the arrow $U \xhookrightarrow{} V$ to $\mathrm{res}^V_U\colon \mathscr{F}(V) \to \mathscr{F}(U)$, which we call the restriction maps. Elements of $\mathscr{F}(U)$ are called sections of $\mathscr{F}$ over $U$.
The main example I always keep in mind is the presheaf $\mathscr{F}$, where $\mathscr{F}(U)$ is the set of continuous functions on $U$. Indeed, since a presheaf really has all the data of a topological space, this is a very natural presheaf to think about. For shorthand, I will sometimes write $\mathrm{res}^V_U(f) = f|_U$, corresponding with the function notation.
In fact, the presheaf of continuous functions has some more useful properties, which motivate the definition of a sheaf.
Definition (Sheaf).
A presheaf is a sheaf that satisfies the following axioms: Let $\{U_i\}_{i\in I}$ be an open cover of $U$.
- (Identity axiom) Let $f_1,f_2\in \mathscr{F}(U)$. If $f_1|_{U_i} = f_2|_{U_i}$ for all $i\in I$, then $f_1=f_2$.
- (Gluability axiom) Let $f_i \in \mathscr{F}(U_i)$ such that $f_i|_{U_i\cap U_j} = f_j|_{U_i\cap U_j}$ for all $i,j\in I$. Then there exists a $f \in \mathscr{F}(U)$ such that $f|_{U_i} = f_i$.
If you’ve finished a topology course, you are familiar with these two axioms. If we consider a sheaf whose sections are functions, then the first axiom says that they actually are functions. For example, if $X$ has the discrete topology, it really says that if $f_1(x) = f_2(x)$ for all $x\in X$, then $f_1=f_2$.1 So this means sections only have one output for each input, which is precisely the definition of a function.
The second property is the gluing lemma for open sets.
Exercise (Gluability is unique). Let $f_i \in \mathscr{F}(U_i)$ be sections satisfying the gluability axiom. Show that the glued section $f\in \mathscr{F}(U)$ is unique.
Remark (Categorical sheaf axioms).
The sheaf axioms are the same as the following diagram being exact
$$ \bullet \to \mathscr{F}(U) \to \prod_{i\in I}\mathscr{F}(U_i) \mathrel{\substack{\textstyle\rightarrow\\[-0.6ex] \textstyle\rightarrow}} \prod_{i,j\in I}\mathscr{F}(U_i\cap U_j). $$
Here’s a nice explanation, which I owe to my friend Haran. The maps are defined naturally:
- An section in $\mathscr{F}(U)$ is the same as a map $\bullet \to \mathscr{F}(U)$ ($\bullet$ is the one object category).
- The second map is $\prod_{i\in I}\mathrm{res}^U_{U_i}$.
- There are two maps to each $\mathscr{F}(U_i\cap U_j)$: $\mathrm{res}^{U_i}_{U_i\cap U_j}$ and $\mathrm{res}^{U_j}_{U_i\cap U_j}$. The two maps are defined correspondingly.
Exactness at $\mathscr{F}(U)$ says that if two sections restrict to the same thing for each $i\in I$, then they must have come from the same thing (the image of $\bullet \to \mathscr{F}(U)$). This is the identity axiom.
Exactness at $\prod_{i\in I}\mathscr{F}(U_i)$ says that if we have a collection of sections over each $U_i$ such that $\mathrm{res}^{U_i}_{U_i\cap U_j}$ and $\mathrm{res}^{U_j}_{U_i\cap U_j}$ are the same for the corresponding sections where those restrictions make sense, then they must have come from some section in $\mathscr{F}(U)$. This is the gluability axiom.
Morphisms of sheaves
We want to make (pre)sheaves a category, so we need to define morphisms.
Definition (Morphism of (pre)sheaves).
Let $\mathscr{F},\mathscr{G}$ be presheaves of sets (abelian groups, rings, etc.) on a topological space $X$. Let $\phi\colon \mathscr{F} \to \mathscr{G}$ represent the maps $\phi(U)\colon \mathscr{F}(U) \to \mathscr{G}(U)$ for all open $U \subseteq X$ such that it behaves nicely with restriction maps. That is, for an inclusion $U\xhookrightarrow{} V$, the following diagram commutes:
$$ \begin{CD} \mathscr{F}(V) @>\phi(V)> > \mathscr{G}(V) \\ @V{\mathrm{res}^V_U}VV @VV{\mathrm{res}^V_U}V \\ \mathscr{F}(U) @>\phi(U)> > \mathscr{G}(U) \end{CD} $$
We call $\phi$ a morphism of presheaves. If $\mathscr{F}$ and $\mathscr{G}$ happen to be sheaves, it is a morphism of sheaves.1
C.f., a homomorphism of abelian groups is a homomorphism of groups where the groups just happen to be abelian. Generally, this says the category of sheaves is a subcategory of the category of presheaves. ↩︎
A presheaf that is not a sheaf
I’ll introduce the main example in the text of a presheaf that is not a sheaf. It will be somewhat unintuitive to think of presheaves that do not satisfy the identity axiom. Indeed, if the sections of a sheaf are functions, we can define the restriction map $\mathrm{res}^U_V$ as restricting a function on $U$ to $V$. This sheaf satisfies the identity axiom. We’ll try to find a sheaf of functions that fails gluability.
Example (Logarithms???).
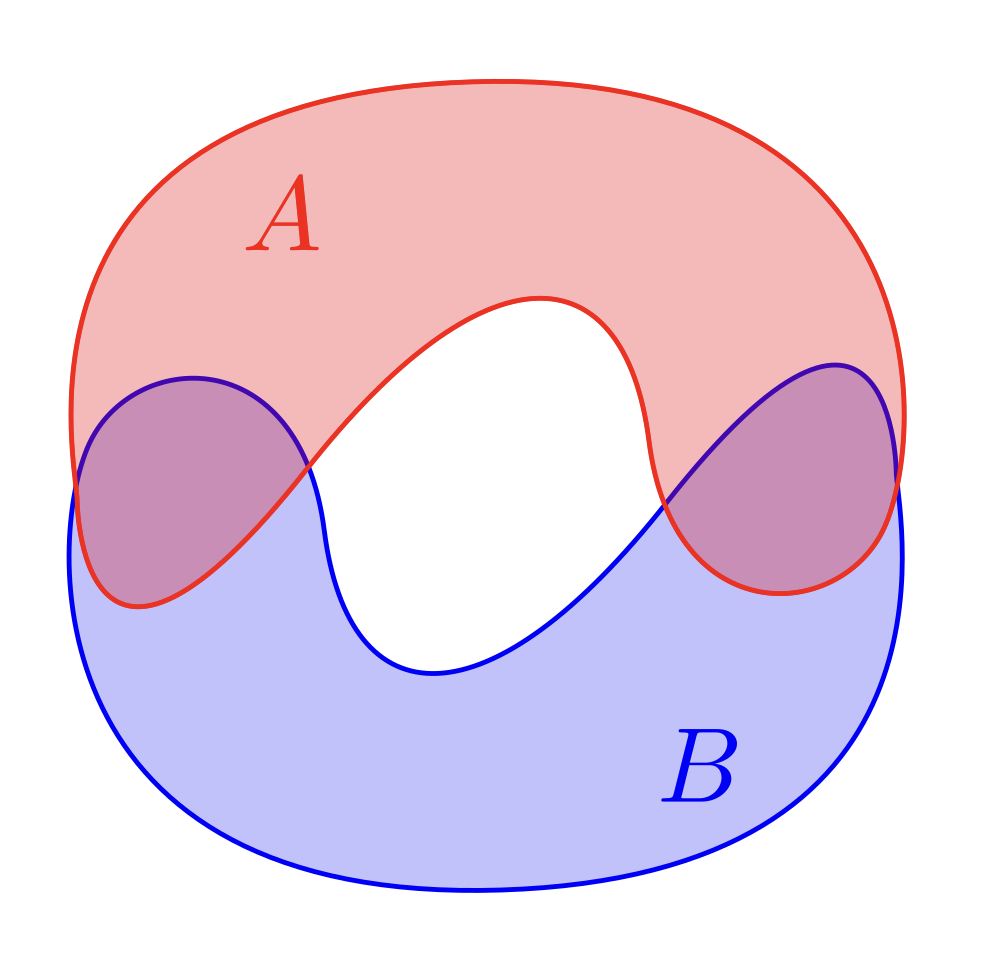
First, a quick return to algebraic topology. We know that simply-connected spaces are not closed under unions. Proof by picture:
($\pi_1(A) = \pi_1(B) = 0$, but $\pi_1(A\cup B) = \Z$). Therefore, if we got a presheaf of “functions that are only defined on simply-connected regions,” then it would not be a sheaf.
Such an example comes out of complex analysis:
Theorem. Let $\Omega \subseteq \mathbb{C}$ be a simply-connected open set with $0\notin \Omega$ and $1\in \Omega$. Then there is a branch of the logarithm on $\Omega$: $F(z) = \log_{\Omega}(z)$ such that
- $F$ is holomorphic on $\Omega$,
- $e^{F(z)} = z$ for all $z\in \Omega$,
- $F(r) = \log{r}$ on the real axis near $1$.
The idea with the proof is to let $F$ be the primitive of $1/z$ in $\Omega$. This is well-defined because $0\notin \Omega$, so we may define
$$ F(z) := \int_{\gamma}\frac{1}{z}dz, $$
where $\gamma$ is any curve from $1$ to $z$. We use simply-connectedness to guarantee this integral makes sense (for example, if the region was $\mathbb{C}-\{0\}$, then the trivial loop gives the value $0$, but the loop around the singularity at $\{0\}$ gives $2\pi i$ by the residue theorem).
So here’s our example: let $\mathscr{F}$ be the presheaf of functions that admit a holomorphic logarithm. The presheaf checks are clear, since we are working with a presheaf of functions. However, there exist log branches of $z$ in the simply-connected regions
$$ (\mathbb{C}-\{0\}) \cap \{z : \mathrm{Im}(z) > -0.01\}, \qquad(\mathbb{C}-\{0\}) \cap \{z : \mathrm{Im}(z) < 0.01\}, $$
but not in their union $\mathbb{C}-\{0\}$. Indeed, it would be the primitive of $1/z$, so over the circle $S^1$ (oriented counter clockwise),
$$ \int_{S^1}\frac{1}{z} = F(1) - F(1) = 0. $$
On the other hand, one can compute directly
$$ \int_{S^1}\frac{1}{z} = 2\pi i. $$
So no such logarithm exists, and the gluability axiom fails.
Example.
A similar result to the previous theorem is that if $f\colon \Omega \to \mathbb{C}$ is a non-zero holomorphic function on a simply-connected open set $\Omega \subseteq \mathbb{C}$, then it admits a holomorphic logarithm.
The proof comes from defining the logarithm $g$ as
$$ g(z) := \int_{\gamma}\frac{f^\prime(w)}{f(w)}dw. $$
Well-definedness comes from simply-connectedness and $f$ being nonzero.
I’ll now fit this example in a general framework. Let $\mathscr{O}_\mathbb{C}$ be the sheaf of holomorphic functions, $\mathscr{O}_\mathbb{C}^*$ the sheaf of nonzero holomorphic functions, and $\underline{\Z}$ be the constant sheaf (sections are locally constant maps $U\to \Z$). Then we have a sequence of sheaves of abelian groups
$$ 0 \to \underline{\Z} \xrightarrow{\times 2\pi i} \mathscr{O}_{\mathbb{C}} \xrightarrow{\exp} \mathscr{O}_{\mathbb{C}}^* \to 1. $$
However, this fails to be short exact on sections for the same reason as before: on $\mathbb{C}-\{0\}$, the nonzero function $z$ does not admit a holomorphic logarithm, so the last map is not surjective! So our previous example was just the image presheaf of $\mathscr{O}_{\mathbb{C}}$.
This sequence is nearly short exact. If $U$ is simply-connected, then the maps of sections form a short exact sequence by the previous theorem.
We notice that locally (on germs), the map is surjective, so we may need to define a new notion of exactness. This leads to sheafification.
Silly remarks
I wrote this blog post over spring break, and I hoped to include more examples of presheaves that were not sheaves so that I could better understand sheafification. As I progressed through the chapter, I realized that the one example Vakil gives seems the most geometric. I did come up with some honorable mentions though
- Any presheaf where the condition on sections is related to counting, e.g., the presheaf of real-valued functions on $\R^n$ exactly one zero is not a sheaf. In fact, the presheaf of real-valued functions on $\R^n$ with finitely many zeros is not a sheaf.
- On a non-orientable manifold $M$ (e.g. a Möbius band), let sections over $U$ be non-vanishing top forms. Warning: this is actually a sheaf, since the gluing axiom does actually hold for $k$-forms on manifolds. I was hoping this would fail for similar reasons to the logarithms example, since a non-orientable manifold is the union of orientable manifolds.
Some motivation for the Zariski topology
People who have been though classical algebraic geometry are immediately told about the Zariski topology, which, for example, give a topology to $k$ for any field $k$.
Let’s look at the field $\R$. Perhaps naively, we try to use the regular topology $\mathcal{T}_{\rm{reg}}$ (i.e. the one you learn in analysis: open sets are sets where every point is interior) to form a sheaf, where the sections over $U \subseteq \R$ are polynomials in $\R[x]$ restricted to $U$.
However, gluability fails again! The problem is that we are letting too many sets be open. For example, consider the intervals $\dots,(-1,1),(1,3),(3,5)\dots$. On $(n-1,n+1)$, the polynomial $x-n \in \R[x]$ has one zero and is not identically zero. However, we vacuously should be able to glue these polynomials, since the intervals $\{(n-1,n+1) : n \in 2\Z\}$ are disjoint. On the other hand, such a section has infinitely many zeros but is nonzero, which is impossible for a polynomial.
If we instead equip $\R$ with the Zariski topology $\mathcal{T}_{\rm zar}$, we know that closed sets are either $\R$ or finite sets, so we won’t be able to union infinitely many disjoint sets as before. In fact, we actually do get a sheaf. One possible explanation is analytic: if we have two sections $p_1, p_2$ over the open sets $U_1,U_2$, respectively, then they agree on all but finitely many points. But $p_1$ and $p_2$ are restrictions of continuous functions on $\R$, so they must arise from restricting the same underlying function. We’re essentially adding the removable discontinuities back.
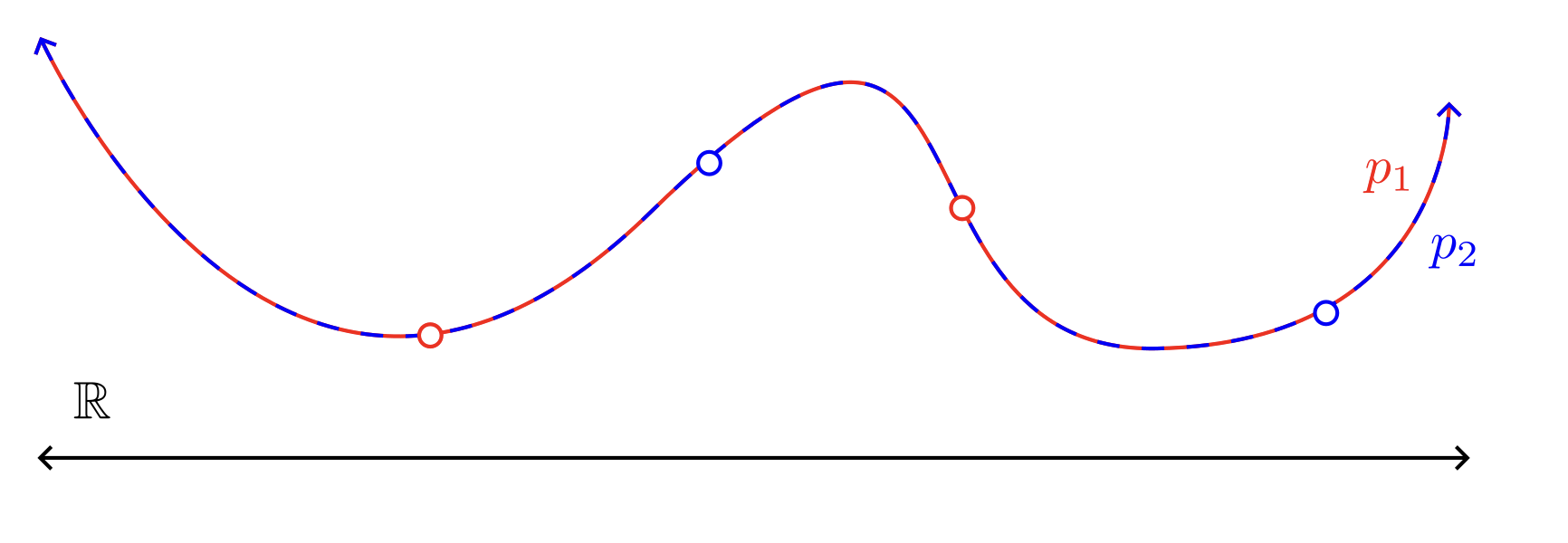
The sections $p_1$ and $p_2$ clearly arise from the same continuous function.
Of course, if the topology is not discrete, then the property becomes more subtle. ↩︎