Why homology is weaker than homotopy
The main two flavors of invariants in an introductory algebraic topology class are the homology groups associated with a space and the homotopy groups (typically just the first homotopy group, $\pi_1$). The fundamental group is formed by looking at loops starting at a certain point. Similarly, the homotopy groups look at cycles, which can be thought of as loops that commute. Because of these similarities, I wondered about which one was “better” at differentiating topological spaces.
Formally, here is the statement I wanted to figure out:
Problem. Are there finite-dimensional, connected, compact CW-complexes $X$ and $Y$ with the same homology groups $H_k(X)\cong H_k(Y)$ for all $k$ that do not have the same fundamental groups $\pi_1(X)\ncong\pi_1(Y)$?
My first clue was from our professor telling us that “the first homology group is just the abelianization of the fundamental group.” Well, I know plenty of groups that aren’t their abelianization; I just need to find a space $X$ with $\pi_1(X)$ a non-abelian group!
Are there any cases in 0 or 1 dimensions?
For $0$ dimensions, there is only one such complex: a point—so we have no hope there.
We can start experimenting with $1$-dimensional complexes, but then we’ll notice that the first homology group and the fundamental group both just count the number of holes in different ways. That is, if $X$ has $n$ holes, then
$$ \pi_1(X)\cong \mathbb{Z}^{*n} = \underbrace{\mathbb{Z} * \cdots * \mathbb{Z}}_{n \text{ times}} $$
(where $*$ is the free product operation on groups) and $H_1(X)\cong \mathbb{Z}^n$, so we have no luck here either.
2-dimensional complexes
For homology, I would like something very simple, like all homology groups being free modules. The two groups $\mathbb{Z}^{*2}$ and $\mathbb{Z}^2$ both have abelianization $\mathbb{Z}^2$, so it would be nice to find spaces with these as their fundamental groups. For readers comfortable with algebraic topology, I encourage you to find these spaces before continuing.
Finding a space with fundamental group $\mathbb{Z}^2$ should be easy from the following fact about fundamental groups:
(I should have included base points before, but these spaces are path-connected, and I’m not concerned about the precise maps for isomorphisms).Lemma (Fundamental group of products).
Let $x_0\in X$ and $y_0\in Y$. Then
$$ \pi_1(X\times Y, (x_0,y_0)) \cong \pi_1(X,x_0)\times \pi_1(Y,y_0). $$
From this lemma, we get the fact that the torus $X=S^1\times S^1$ has fundamental group $\pi_1(S^1)\times \pi_1(S^1)\cong \Z\times \Z$.
As discussed in the previous section, $1$-dimensional space with $2$ holes (the figure eight space), which is our $Y$, has fundamental group $\Z*\Z$.
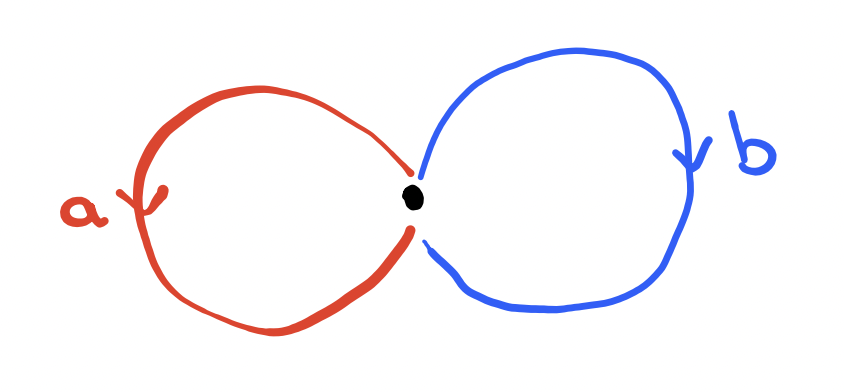
The figure eight space with its two generating loops $\color{red} a$ and $\color{blue}b$.
So (with the appropriate CW-complex), $H_1(X)\cong H_1(Y)\cong \Z^2$.
We would be so close to done if we didn’t require that all homology groups had to be equal. We have no issues with $H_0$ because both spaces are connected (and so $H_0(X)\cong H_0(Y)\cong \Z$), but $H_2(X)$ is not trivial, while $H_2(Y)$ is trivial (by it being a one-dimensional CW-complex).
Fixing the example
But we still have some tools from homology that could make the second homology groups match.
Definition (Wedge sum).
Let $X$ and $Y$ be CW-complexes and let $x_0\in X$, $y_0\in Y$. Then the wedge sum of $X$ and $Y$ is formed by taking $X\sqcup Y/\sim$, where $\sim$ is an equivalence relation generated by $x_0\sim y_0$ and nothing else. Denote this space $X\vee Y$.
In other words, $X\vee Y$ is formed by identifying $X$ and $Y$ at a single point.
Lemma (Homology of wedge sum).
Let $X$ and $Y$ be CW-complexes. Then
$$ H_k(X\vee Y) \cong \begin{cases} H_k(X) \oplus H_k(Y) &\text{if }k>0, \\ \Z &\text{if }k=0. \end{cases} $$
Lemma (Homology groups of $n$-sphere).
Let $S^n$ be an $n$-sphere. Then
$$ H_k(S^n) \cong \begin{cases} \Z & \text{if }k=0 \text{ or }n, \\ 0 & \text{otherwise.} \end{cases} $$
Those who I asked this question (thank you!) gave me the helpful takeaway from these two lemmas: the $n$-spheres $\{S^n\}$ form something like a basis for spaces with free homology groups when taking wedge sums. More precisely, if a connected, $n$-dimensional CW-complex $Z$ has homology groups $H_k(Z) \cong \Z^{z_k}$, then the space
$$ (S^1)^{\vee z_1}\vee (S^2)^{\vee z_2} \vee\cdots \vee (S^n)^{\vee z_n} $$
has the same homology groups (where $X^{\vee z}=\underbrace{X\vee \cdots \vee X}_{n \text{ times}}$).
So let’s finally finish the problem. We know the torus $T^2\cong S^1\times S^1$ has homology groups
$$ H_k(T^2) = \begin{cases} \Z &\text{if } k = 0, \\ \Z^2 &\text{if } k = 1, \\ \Z &\text{if } k = 2, \\ 0 &\text{otherwise.} \end{cases} $$
From before, the space $(S^1)^{\vee 2}\vee S^2 \cong S^1\vee S^1\vee S^2$ also has the same homology groups. This space looks like the figure eight space with a sphere attached. But a sphere is simply connected, making it have no affect on the fundamental group, so $\pi_1(S^1\vee S^1\vee S^2) \cong \Z*\Z$, which is not $\Z\times \Z$, and we are done.
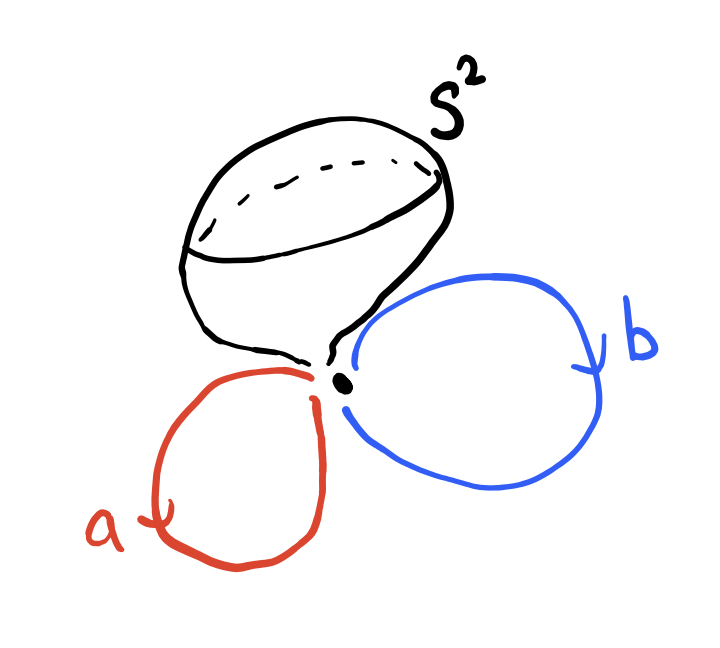
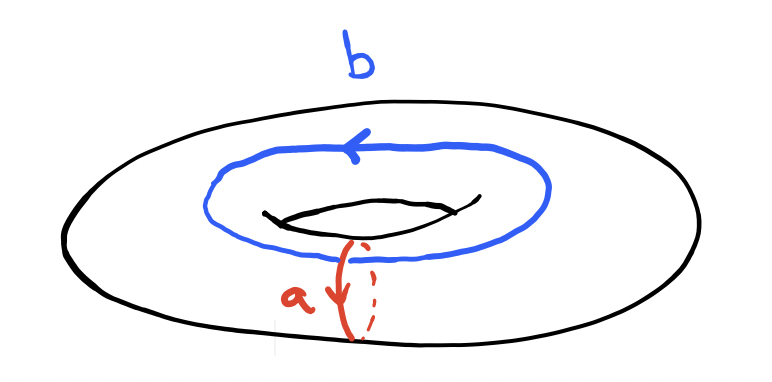
Comparing the two cycles that generate the first homology and fundamental groups.
A harder question
An undergrad I talked to about this proposed another question that may be interesting.
Problem (Trivial homology groups). A topological space is called acyclic if its homology groups match those of a single point. In our case, this is if all the homology groups are trivial for $k>0$. Are there two acyclic (finite-dimensional, connected, compact) CW-complexes with different fundamental groups?
As a starting point, this means that the fundamental groups will have to have a trivial abelianization. In other words, the commutator subgroup of the fundamental group is the whole group. Such groups are called perfect.
There’s also a question about the minimal dimension for a counterexample.
Problem. Are there two acyclic $2$-dimensional CW-complexes with different fundamental groups?