Visualizing prime spectrums with graphs
In Atiyah and Macdonald’s book we construct a certain topological space from a ring called the prime spectrum of a ring. While working through the exercises, I saw an interesting way of viewing closed and open subsets of the prime spectrum that borrowed ideals from combinatorics.
What is the prime spectrum of a ring?
Definition (Prime ideal).
An ideal $\mathfrak{a}$ of a ring $A$ is a subring (a subset of $A$ that is still a ring under $A$’s operations) that has the property that any $a\in A$ times $p\in \mathfrak{a}$ has $ap\in \mathfrak{a}$ as well. That is, the elements in the ideal stay in the ideal after multiplying by any element of $A$.
If an ideal $\mathfrak{p}$ is such that $pq\in \mathfrak{p}$ implies $p\in \mathfrak{p}$ or $q\in \mathfrak{p}$, then the ideal is said to be a prime ideal.
Take a moment to understand where the name prime comes from. For example, the prime ideals of $\mathbb{Z}$ are precisely the ideals generated by the primes.
Definition (Prime spectrum). The prime spectrum of a ring $A$, denoted $\mathop{\mathrm{Spec}}(A)$, is the set of all prime ideals of $A$.
Creating a topology on $\mathop{\mathrm{Spec}}(A)$
Looking at this set isn’t very interesting on its own. However, if we look at the sets $$ V(E)\coloneqq\{\mathfrak{p}:\mathfrak{p} \text{ is a prime ideal that contains } E\} \subseteq \mathop{\mathrm{Spec}}(A), $$ for every $E \subseteq A$, we can prove that these satisfy the conditions for closed sets in a topology. We call this topology the Zariski topology. We see this topology appear frequently in algebraic geometry.
Open sets are precisely the complements of these closed, sets, and we can show that $X_f\coloneqq \mathop{\mathrm{Spec}}(A)-V(f)$ for $f\in A$ forms a basis for the Zariski topology (that is, every open set can be written as the union of these sets $X_f$). These $X_f$ are called basic open sets.
Visualizing $\mathop{\mathrm{Spec}}(A)$
The topology on $\mathop{\mathrm{Spec}}(A)$ can vary greatly depending on the ring, and finding a good way to visualize it in general was tough. However, a special property of these open sets motivated a specific visualization.
Posets and Hasse diagrams
Definition (Order).
An order gives us a way to order elements of a set. For example, the integers have an order, $\leq$. An order $\leq$ must satisfy the following properties:
- Reflexivity: $a\leq a$,
- Antisymmetry: $b \leq a$ and $a \leq b$ implies $a=b$,
- Transitivity $a\leq b$ and $b\leq c$ implies $a\leq c$.
We can observe that $\leq$ (less than on equal to) is an order on the integers.
Definition (Poset). A partially ordered set (poset) is a set that has a partial order. A partial order is an order where not every element can be compared, i.e. we allow $a\nleq b$ and $b\nleq a$.
An example of partial orders that is useful for the visualization is the inclusion order on a collection of subsets of $A$, denoted $\subseteq$. We define it how one would expect: $B \subseteq C$ if $B$ is contained in $C$. This is only a partial order because, for example, $\{1,2\}$ and $\{3,4\}$ are incomparable in this order.
A Hasse diagram is a visualization of a poset, often used in combinatorics, which was where I first heard about them. In terms of the inclusion order, we draw an arrow from $B$ to $C$ if $B$ is contained in $C$.
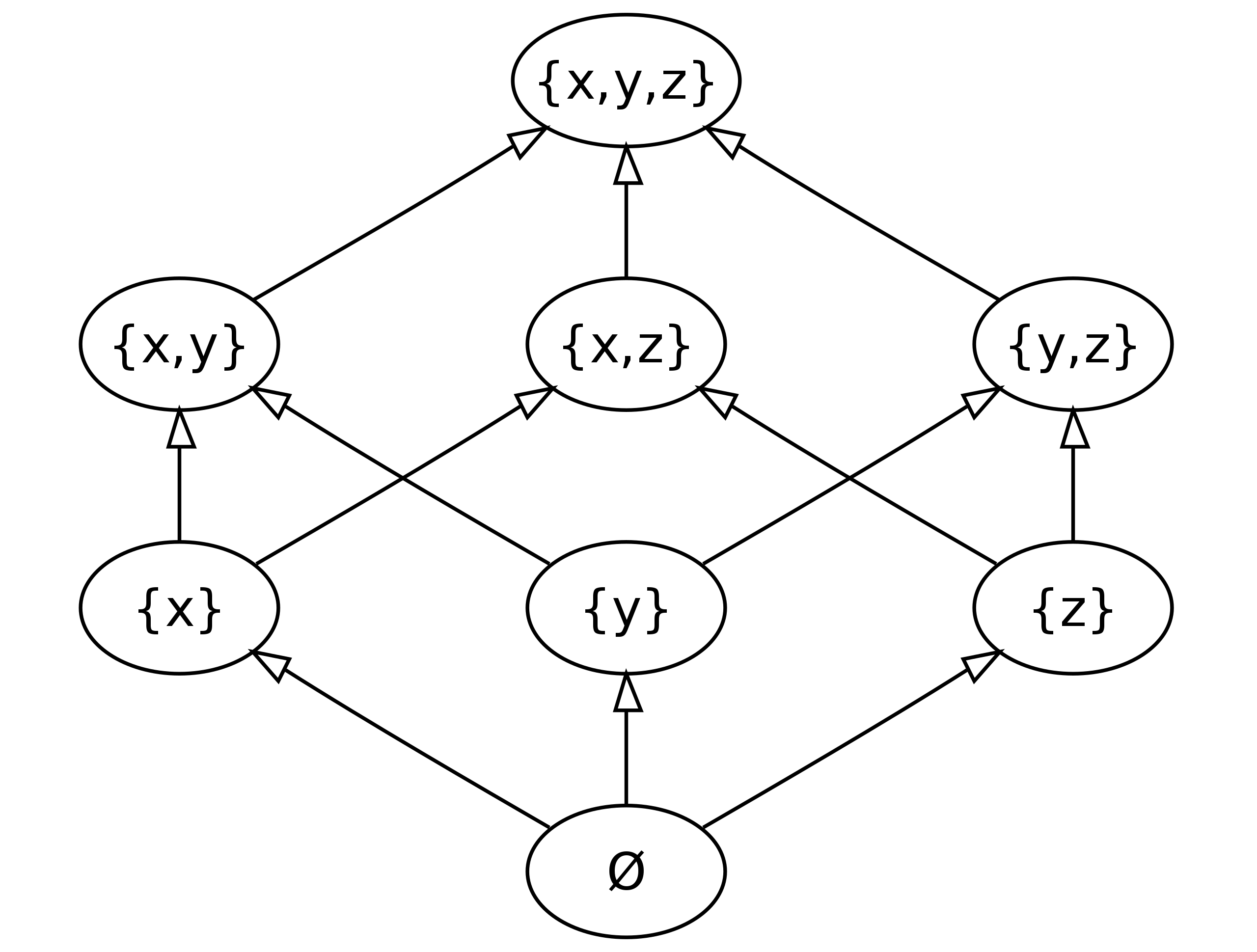
Figure 1. The Hasse diagram of all subsets of $\{x,y,z\}$. By I, KSmrq, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2118211
Since $\mathop{\mathrm{Spec}}(A)$ is a collection of subsets of $A$, we can similarly create a Hasse diagram. For example, lets start with the Hasse diagram of $\mathop{\mathrm{Spec}}(\mathbb{Z})$. As I said previously, the prime ideals of $\mathbb{Z}$ are precisely the ideals generated by primes, which we will denote $(p)$. Additionally, the trivial ideal, $(0)$ is also prime. Since $(p)=\{\dots,-2p,-p,0,p,2p,\dots\}$ it contains no other prime ideals other than $(0)$. Thus, the Hasse diagram looks as follows.
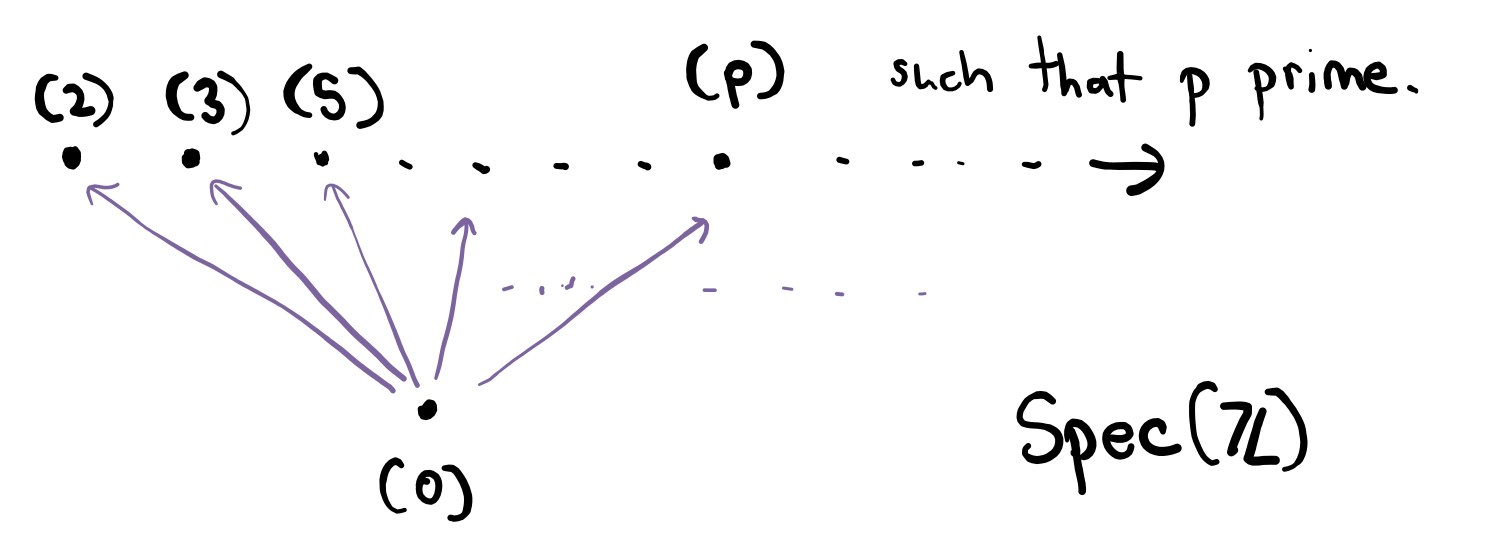
Figure 2. The Hasse diagram of $\mathop{\mathrm{Spec}}(\mathbb{Z})$.
Topological properties visualized in Hasse diagrams
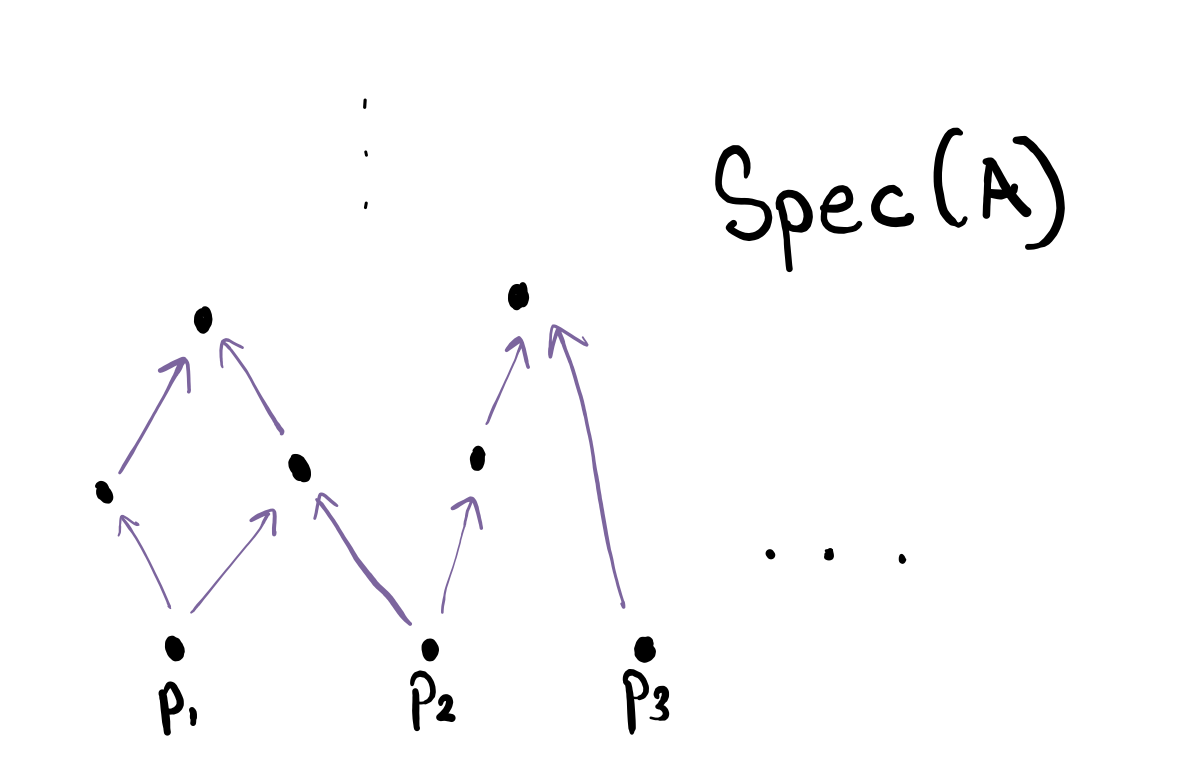
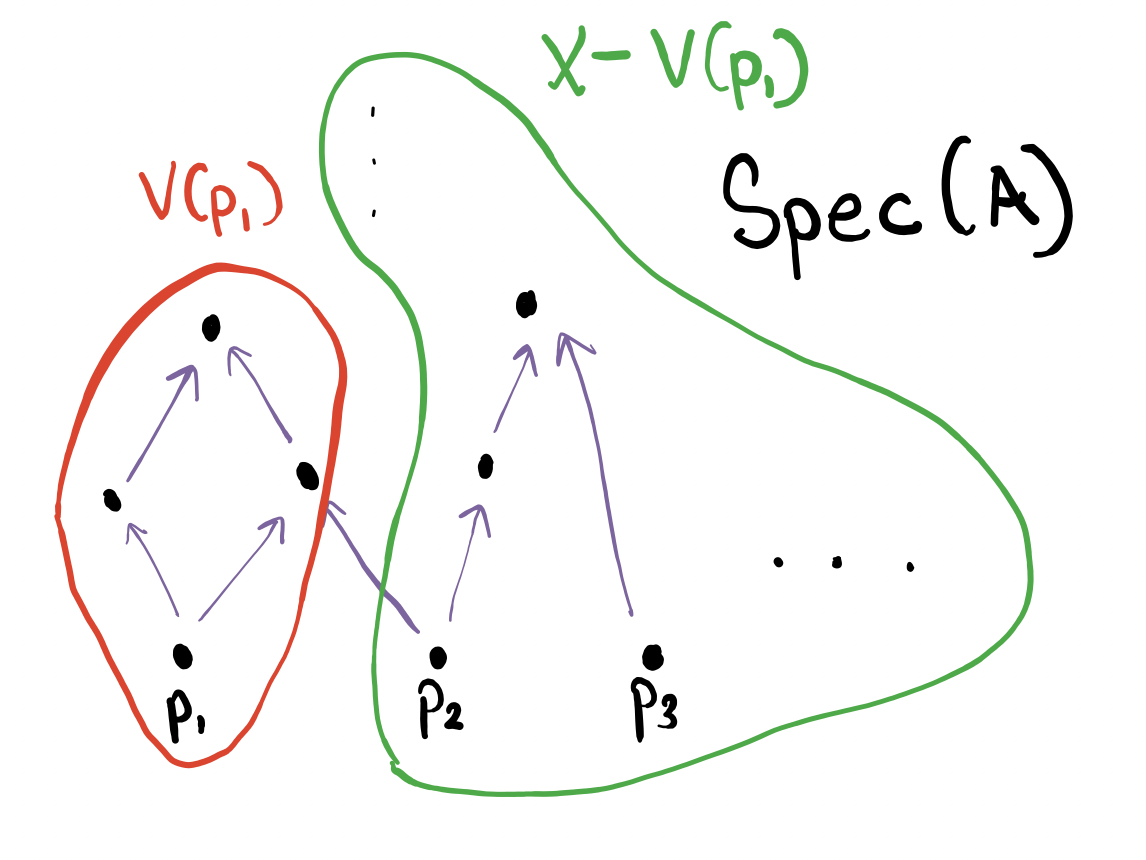
Let $X=\mathop{\mathrm{Spec}}(A)$. Recall our definition of a closed set: all prime ideals that contained a subset $E$ of $A$. If $E$ is a prime ideal, we can easily visualize what $V(E)$ is. Let $E=\mathfrak{p}_1$ in the following diagram.
Then to find $V(E)$, we simply have to travel “up” from $E$ and see what sets we hit, since the only ideals that contain that prime ideal are above it.
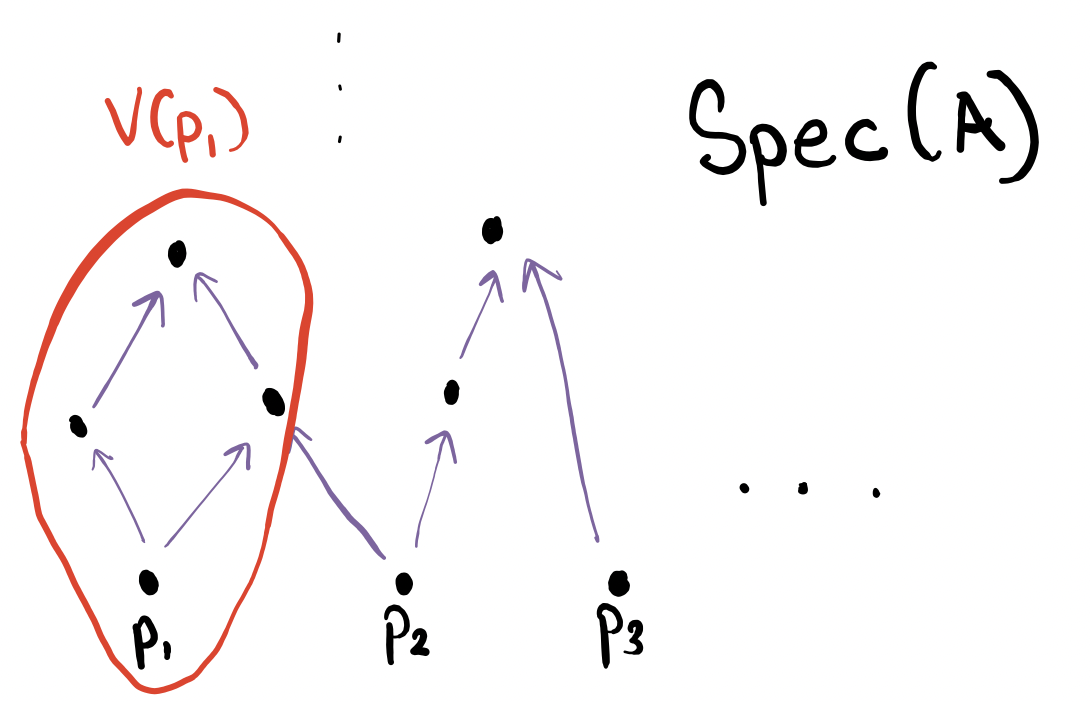
The open set (the complement of $V(E)$) is precisely the rest of the elements.
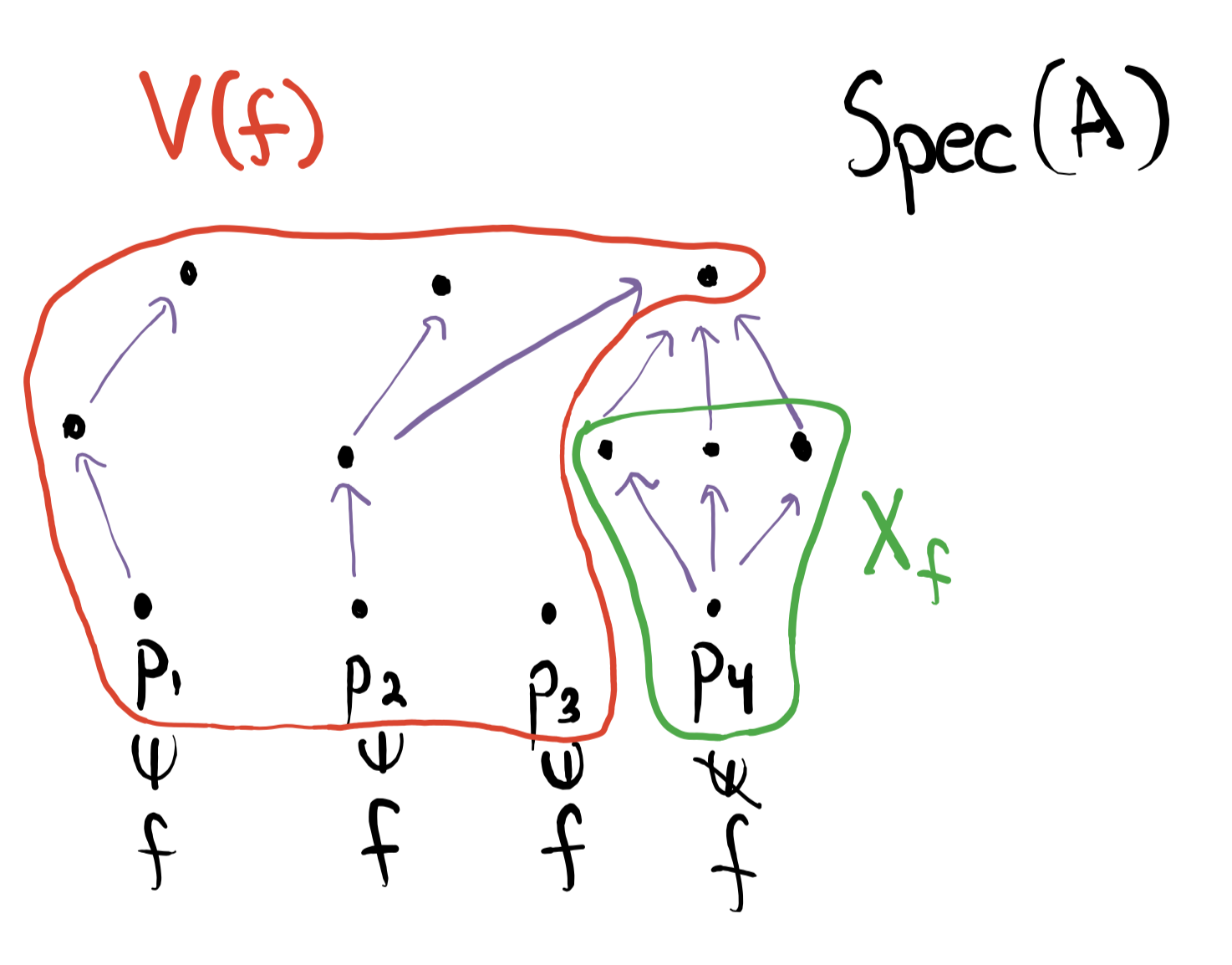
If we want to find $V(f)$ for $f\in A$, all we have to do is find all the minimal prime ideals – the prime ideals that do not contain any other prime ideals ($\mathfrak{p}_1$, $\mathfrak{p}_2$, and $\mathfrak{p}_3$ in our figure) in the previous figure – that contain $f$, and expand upwards.
Applying this to a problem
Problem. Show that for $\mathfrak{p}\in \mathop{\mathrm{Spec}}(A)$, $\overline{\{\mathfrak{p}\}} = V(\mathfrak{p})$.
To solve this, we use the definition of a closure: the closure of a set $S$ is $S$ together with all its limit points. Consider any prime ideal $\mathfrak{q} \neq \mathfrak{p}$. If $\mathfrak{q}\in V(\mathfrak{p})$, then it contains $\mathfrak{p}$. Let’s draw a sketch of what an open neighborhood of $\mathfrak{q}$ would look like.
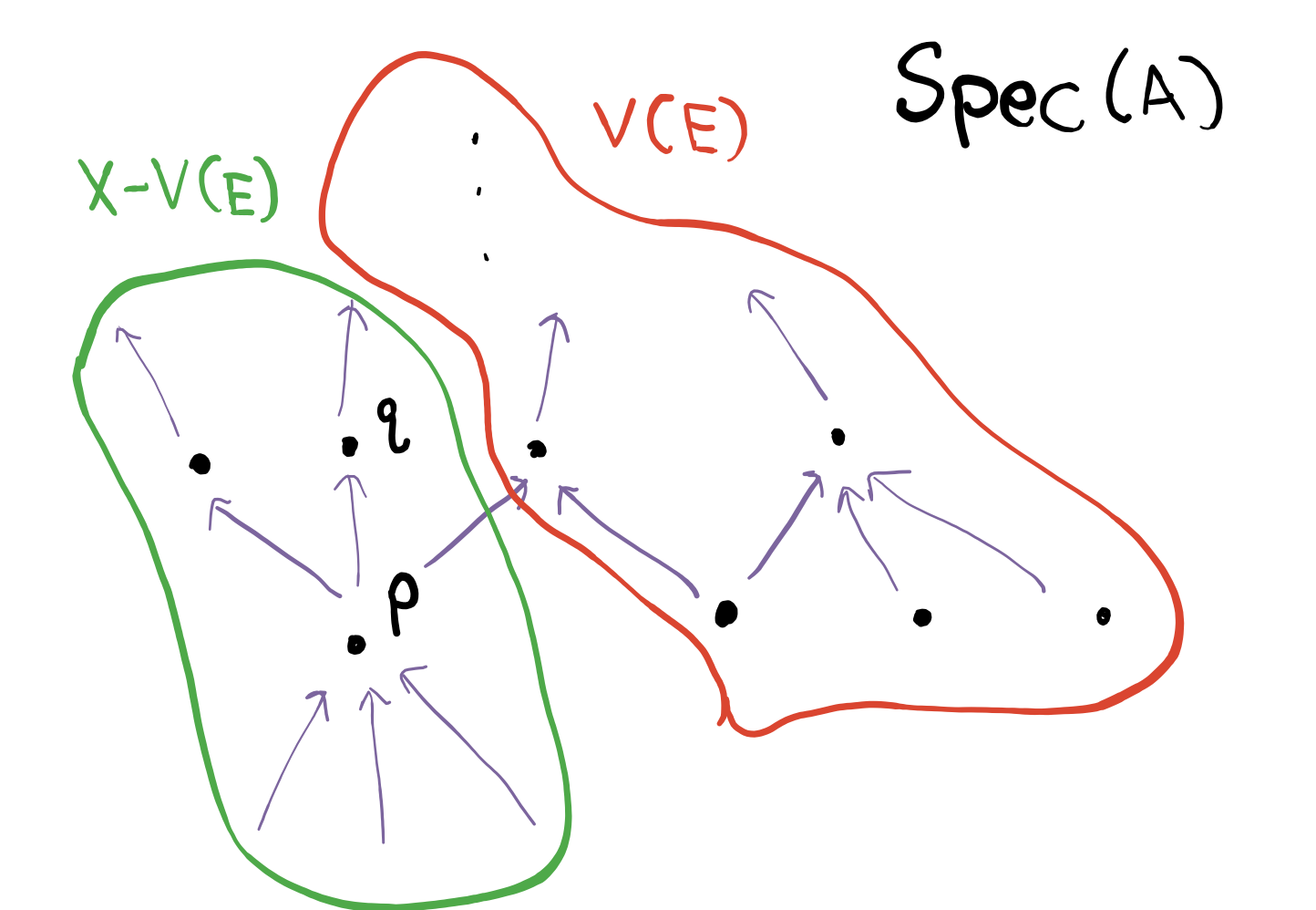
We can easily see that all subsets of $\mathfrak{q}$ are contained in that open set too ($\mathfrak{q}$ “guards” its subsets from being in $V(E)$). In particular, that includes $\mathfrak{p}$. Thus, we have intuition that $\mathfrak{q}$ is a limit point.
Conversely, if $\mathfrak{q}$ does not contain $\mathfrak{p}$, then in particular, $X-V(\mathfrak{p})$ is an open neighborhood of $\mathfrak{q}$ that does not contain $\mathfrak{p}$, making $\mathfrak{q}$ not a limit point of $\{\mathfrak{p}\}$.
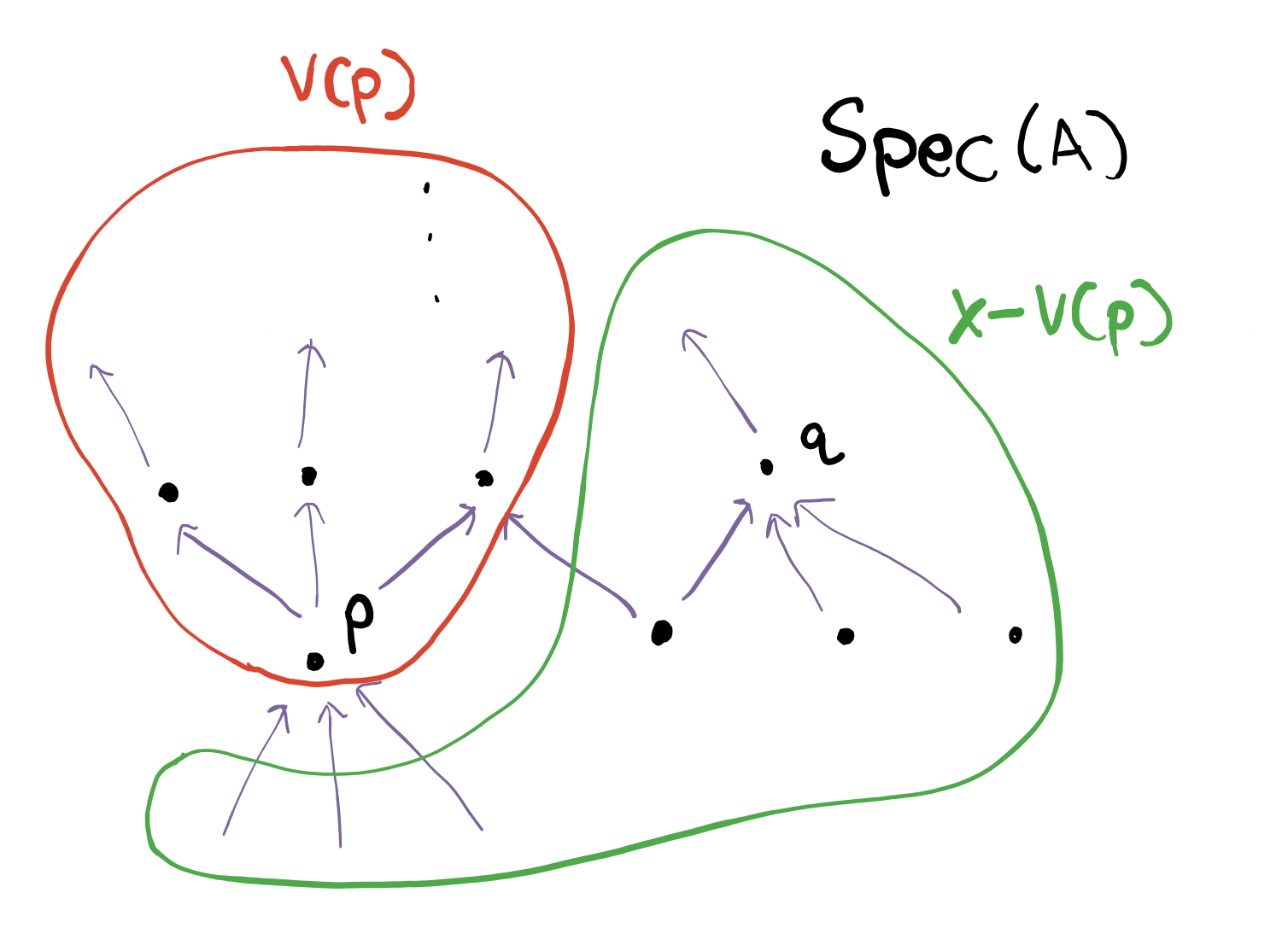
Thus, we have solved the problem.
Finally, to connect this to our example of $\mathop{\mathrm{Spec}}(\mathbb{Z})$, a point $x$ in a topological space is called a generic point if the closure of $\{x\}$ is the whole space. Since $\overline{(0)}=V((0))=\mathop{\mathrm{Spec}}(\mathbb{Z})$, we can see that $(0)$ is a generic point. Many visualizations of $\mathop{\mathrm{Spec}}(\mathbb{Z})$ showcase this by having $(0)$ vaguely overlaid around all the other points in the set, since it is “close” to every point.
In the Hasse diagram, $(0)$ is under all the ideals. The closure of $\{(0)\}$ “expands” $(0)$ upwards, which shows us that it is “close” to all of them.